2022. 3. 11. 18:56ㆍSTUDY/머신러닝
분류모델 - KNN
KNN의 기본개념
KNN 알고리즘은 분류와 회귀문제를 둘다 해결할 수 있는 머신러닝 알고리즘이다.
KNN 알고리즘을 한마디로 표현하면 "Birds of a feather flock together. (유유상종)" 이라고 할 수 있다.
즉 비슷한 특성을 가진 데이터끼리 모여있다는 것 을 전제로 하고, 새로운 데이터가 들어왔을때
주변 데이터를 참고하여 어느 분류에 속하는지 학습하는 것이다.
KNN에서 K는 새로운 입력데이터의 주변에서 몇개의 데이터를 볼것인가? 라는 의미를 가지고 있다.

아래 빨간색원이 입력데이터로 들어왔을때
K=3 일경우 주변에 세개의 원을 고려하였고 --> Class B
K=6 일경우 주변에 여섯개의 원을 고려하였음. --> Class A
K값에 따라 Class를 다르게 판단 할 수 있는데 적절한 K값을 지정하는게 중요하다.
K값이 너무 작으면 이상치를 탐지할 수 없고
K값이 너무 크면 올바른 분류를 할 수없을것이다.
KNN은 거리를 기반으로 하는 모델이다.
새로운 입력데이터가 들어왔을때 주변 데이터를 참고하여, 유사한쪽으로 클래스를 분류해준다 하였다.
여기서 유사함의 기준은 "거리"로써 흔히 유클리드 거리와 맨해튼거리를 사용한다.
1. 유클리드 거리
유클리드 거리는 일반적으로 우리가 배운 점과 점사이의 거리를 구하는 방법이다.
d(A,B)=(x2−x1)2+(y2−y1)2

2. 맨해튼 거리
맨해튼 거리는 점과 점사이의 직선거리가 아니라, X축과 Y축을 따라 간 거리를 의미한다.
따라서 두 포인트사이의 거리는 (x좌표 차이) + (y좌표 차이)로 단순히 정의된다.

KNN 사용 시 스케일링이 꼭 필요하다.
두 독립변수를 두고, 거리기반의 중요도 측정을 하였을 때,
하나의 독립변수의 값의 범위가 엄청 클경우 해당 독립변수에 치중되어 거리해석이 될 가능성이 높다.
따라서 스케일링을 통해동일한 범위값으로 지정해주어야 한다.
1. 최소 - 최대 정규화 ( min-max scaling )
해당방법은, 변수값의 범위를 0~1 로 둘 수 있다.
식 : Z=(X−min(X))/(max(X)−min(X))
2. z-score standardization
z-점수 표준화는 변수의 범위를 정규분포화하여 평균을 0, 표준편차가 1이 되도록 한다.
scikit-learn에서 KNN을 지원해준다. (링크 : https://scikit-learn.org/stable/modules/neighbors.html#neighbors)
기본 사용법
# 라이브러리
from sklearn.neighbors import NearestNeighbors
import matplotlib.pyplot as plt
import numpy as np# 데이터정의 및 plot
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
plt.scatter(X[:,0],X[:,1])
plt.hlines(0,-3,3,color="red")
plt.vlines(0,-3,3,color="blue")
plt.xlabel("X-axis")
plt.ylabel("Y-axis")
# 객체정의
alg_choice = ["auto","ball_tree","kd_tree","brute"] # auto : default 값
NN = NearestNeighbors(n_neighbors=2, algorithm=alg_choice[1])
# 학습데이터에 fit
NN.fit(X)
# distances, indices 도출
# n_neighbors = 2로 설정했기에, 자기자신과 가까운애 한개만 봄
distances, indices = NN.kneighbors(X)
print(distances,"\n") # 이웃값과 거리
print(indices) # indices = 이웃값의 인덱스NearestNeighbors 수행시 사용할 알고리즘을 지정할 수 있다.
(default 값 : auto-->학습데이터 맞는 알고리즘 자동설정)
각 알고리즘에 대한 자세한 사항 여기를 참고

# 데이터들간의 neighbor 관계도 파악
NN.kneighbors_graph(X).toarray()
분류 : KNeighborsClassifier 사용
Document 일부내용)
Classification is computed from a simple majority vote of the nearest neighbors of each point: a query point is assigned the data class which has the most representatives within the nearest neighbors of the point.
기준 노드로 부터 근접한 이웃노드들중 과반수에 속하는 클래스로 분류됨을 알 수 있다.
만약 데이터가 not uniformly sample 이라면, 고정된 반지름을 기준으로 분류를 수행하는 여기를 사용하는게 좋다.
# 라이브러리
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib.colors import ListedColormap
from sklearn import neighbors, datasets# 데이터로드
iris = datasets.load_iris()
# feature 두개만 사용
Xdata = iris.data[:, :2] # 150 x 2
ydata = iris.target # 150 x 1
# 변수정의
n_neighbors = 15
h = 0.02 # 메쉬의 step size# 실행
cmap_area = ListedColormap(["orange", "cyan", "cornflowerblue"])
cmap_scatter = ["darkorange", "c", "darkblue"]
# 가중치에 따른 결과 도출
# uniform : 기준 노드로부터 모든 이웃노드가 가중치 동일하게 적용됨
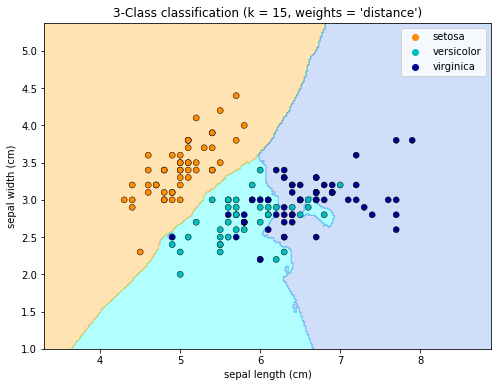
# distance : 기준 노드로부터 가까운 이웃노드가 가중치 크다
for weights in ["uniform", "distance"]:
# 객체정의 및 학습데이터에 fit
KNNclf = neighbors.KNeighborsClassifier(n_neighbors, weights=weights)
KNNclf.fit(Xdata, ydata)
# 메시생성
x_min, x_max = Xdata[:, 0].min() - 1, Xdata[:, 0].max() + 1 # 3.3~8.9
y_min, y_max = Xdata[:, 1].min() - 1, Xdata[:, 1].max() + 1 # 1.0~5.4
x_dim = np.arange(x_min, x_max, h) # (280,)
y_dim = np.arange(y_min, y_max, h) # (220,)
xx, yy = np.meshgrid(x_dim,y_dim) # 둘다 220 x 280
concat_data = np.c_[xx.ravel(), yy.ravel()] # (61600,) x 2 ==> (61600,2)
# 예측
Z = KNNclf.predict(concat_data)
# 영역 plot - 세개의 영역에 대한 색칠
Z = Z.reshape(xx.shape)
plt.figure(figsize=(8, 6))
plt.contourf(xx, yy, Z, cmap=cmap_area, alpha=0.3)
# 학습데이터 점 찍기
sns.scatterplot(
x=X[:, 0],
y=X[:, 1],
hue=iris.target_names[ydata], # 분류값 지정 (인덱스 --> 0:setosa, 1:versicolor, 2:virginica)
palette=cmap_scatter, # 위 분류값 순서에 따른 색깔 지정
alpha=1.0,
edgecolor="black",
)
# plt 설정
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.title(
"3-Class classification (k = %i, weights = '%s')" % (n_neighbors, weights)
)
plt.xlabel(iris.feature_names[0])
plt.ylabel(iris.feature_names[1])
plt.show()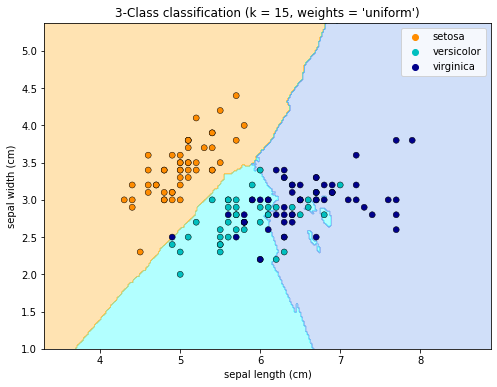
회귀 : KNeighborsRegressor 사용
Document 일부내용)
Neighbors-based regression can be used in cases where the data labels are continuous rather than discrete variables. The label assigned to a query point is computed based on the mean of the labels of its nearest neighbors.
회귀의 경우에는 데이터가 이산형이아니라 연속형이다.
기준 노드에 부여되는 레이블은 해당 노드에 근접한 노드들의 레이블의 평균으로 계산된다
--> K=3이면, 해당노드로 이웃2개를 참고하고, 각 좌표값의 평균을 낸다는 의미인거 같다.
만약 데이터가 not uniformly sample 이라면, 고정된 반지름을 기준으로 회귀를 수행하는 여기를 사용하는게 좋다.
import numpy as np
import matplotlib.pyplot as plt
from sklearn import neighbors
# 데이터생성
np.random.seed(20)
X = np.sort(10 * np.random.rand(50, 1), axis=0) # 0~10 까지의 50 x 1 랜덤 데이터생성
y = np.sin(X).ravel()
# y값에 노이즈추가 : 1차원배열이며, 5개당 한개씩 노이즈추가 (맨 좌측열)
y[::5] += 1 * (0.5 - np.random.rand(10))
# ----- 원리확인위함 -----
yy = [y[0],y[1],y[2],y[3],y[4]]
print(f'첫번째 x값에서의 이웃5개의 y값 평균 : {np.mean(yy)}')
# ------------------------
# 변수 지정
n_neighbors = 5
t = np.linspace(0, 10, 300)[:, np.newaxis] # 0~10 까지의 300개 (plot 하기 위함)
# 회귀 수행
plt.figure(figsize=[8,6])
for i, weights in enumerate(["uniform", "distance"]):
KNNreg = neighbors.KNeighborsRegressor(n_neighbors, weights=weights)
KNNreg.fit(X, y)
y_ = KNNreg.predict(t)
# ----- 원리확인위함 -----
if i==0:
print(f'weight 가 uniform일 때: {y_[0]}')
if i==1:
print(f'weight 가 distance일 때: {y_[0]}')
# ------------------------
plt.subplot(2, 1, i + 1)
plt.scatter(X, y, color="blue", label="Train")
plt.plot(t, y_, color="red", label="Prediction")
plt.axis("tight")
plt.legend()
plt.title("k = %i, weights = '%s'" % (n_neighbors, weights))
plt.tight_layout()
plt.show()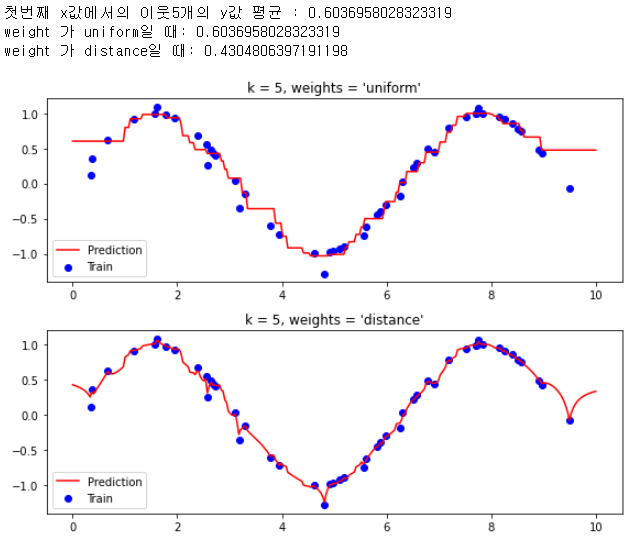
위 코드에서 predict 입력값으로 t를 넣어주었다.
t는 x축 값으로 0~10까지의 300개의 값으로 이루어졌다.
첫 입력은 분명 0일것이고, 0을 입력으로 받아 예측을 수행한다면
x=0과 제일 가까운 점은, fit에서 사용했던 입력데이터 X의 첫번째 값일것이다.
물론 y값은 입력데이터 y의 첫번째 값일 것이다.
그렇다면 predict 의 첫입력에 대한 예측결과값을 보면 0.6036... 이 도출되었다.
해당값은, 학습데이터 첫번째 데이터를 포함한 이웃한 데이터4개에 대한 y값의 평균으로써
위 Document 일부내용) 에 언급한 내용과 일치함을 알 수 있다.
'STUDY > 머신러닝' 카테고리의 다른 글
| [지도학습] 분류모델 - SVM (0) | 2022.03.15 |
|---|---|
| [지도학습] 회귀모델 - 추가내용 ( 비선형회귀 & 학습과정 ) (0) | 2022.03.14 |
| [지도학습] 회귀모델 - 로지스틱 회귀 (0) | 2022.03.14 |
| [지도학습] 회귀모델 - 선형 회귀 (0) | 2022.03.14 |